GM(1,1)灰色预测
显然地,G代表Grey(灰色),M代表Model(模型);而(1,1)代表只含有一个变量的一阶微分方程模型。
灰色系统:
介于黑色和白色之间,部分已知,部分未知,具有小样本数据的不确定性系统。
典型例子:GDP就是灰色系统。
适用赛题:
数列预测
- 特点:定时求量。已知xx年到xx年的数据,请预测下一年的数值。
- 常见GDP、人口数量、耕地面积、粮食产量等问题。
- 针对的问题往往短期波动小、可预测,但长期可能变化大、难以预测。
灾变预测
- 特点:定量求时。已知xx年到xx年的数据和某灾变的阈值,预测下一次灾变发生的时间。
- 常见洪涝灾害、虫灾等问题。
- 模型中需要把超出阈值的数据 (异常数据) 对应的时间组成新序列。
- 拓扑预测
- 特点:对数据波形进行预测。求的是多个模型构成的模型群,等于求解多个灾变预测。
- 与灾变预测类似,不过有较详细的分级,例如虫灾 “轻微” “中度” “重度”。
- 注意事项
- 需要的数据量少,数据量太多了没有意义。
- 只能短期预测,但究竟多短没有严格限制。
以下题为例:某城市1986到1992年道路噪声平均声级数据见下表。请预测下一年的数据。
- 某城市交通噪声数据/$dB(A)$
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| 年份 | 1986 | 1987 | 1988 | 1989 | 1990 | 1991 | 1992 |
| 噪声 | 71.1 | 72.4 | 72.4 | 72.1 | 71.4 | 72.0 | 71.6 |
- 特点:数据少,看不出明显规律,适合用灰色预测。
可进行数据的累加,于是有:
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| 年份 | 1986 | 1987 | 1988 | 1989 | 1990 | 1991 | 1992 |
| $x^{(0)}$ | 71.1 | 72.4 | 72.4 | 72.1 | 71.4 | 72.0 | 71.6 |
| $x^{(1)}$ | 71.1 | 143.5 | 215.9 | 288 | 359.4 | 431.4 | 503 |
累加生成序列:$x^{(1)}(k) = \sum_{i=1}^k x^{(0)}(i)$
弱化其随机性,显现其规律性。
此时生成的新序列 $x^{(1)}$ ,看起来像一个指数曲线 (直线)。因此可用一个指数曲线的表达式来逼近这个新序列,相应可构建一阶常微分方程来求解拟合指数曲线的函数表达式。
关于一阶常微分方程,假设 $x^{(1)}$ 满足形式: $\frac{dx^{(1)}}{dt} + ax^{(1)} = u$
- 要预测下一年数值,就需要新序列 $x^{(1)}$ 的表达式,那就要解出微分方程。
- 要解微分方程,就要先知道参数 $a$ 和 $u$
表达式处理
已知的 $\frac{dx^{(1)}}{dt} + ax^{(1)} = u$ 中的数据是离散的,所以应该把 $\frac{dx^{(1)}}{dt}$ 写成 $\frac{\Delta x^{(1)}}{\Delta t}$ .
- $\Delta t = t - (t-1) = 1$,始终为1;而 $\Delta x^{(1)} = x^{(1)}(t)- x^{(1)}(t-1) = x^{(0)}(t)$
- 得到方程$x^{(0)}(t) + ax^{(1)}(t) = u$ ,即 $x^{(0)}(t) = - ax^{(1)}(t) + u$
为了进一步消除数据随机性,将 $x^{(1)}(t)$ 修正为 $z^{(1)}(t)$
- 考虑到原方程中有 $\frac{\Delta x^{(1)}}{\Delta t}$,因此将 $x^{(1)}(t)$ 改为取前后两个时刻的均值更合理。
- 对 $x^{(1)}$ 进行均值生成:$z^{(1)}(t) = 0.5x^{(1)}(t)+0.5 x^{(1)}(t-1),t=2,…,n$,即方程改为 $x^{(0)}(t) = - az^{(1)}(t) + u$ .
- 可用最小二乘法求未知参数。
模型求解
1.最小二乘法求解
- 当前方程 (函数) 为 $x^{(0)}(t) = - az^{(1)}(t) + u$ .
- 最小二乘法就是求出当拟合函数求的值与已知数据的平方差最小时,未知参数的取值。
- 方程矩阵形式 $Y = B U$
- 最小二乘法也就是求 $(Y-BU)^T(Y-BU)$取最小值时的 $U$
- 求解U的估计值为 $\hat{U} = [\hat{a},\hat{b}]^T = (B^T B)^{-1} B^T Y$,即求出参数 $\hat{a},\hat{b}$ .
然后带入原微分方程,求出$\frac{dx^{(1)}}{dt} + \hat{a}x^{(1)} = \hat{b}$ 的解,即 $\hat{x}^{(1)}(k+1) = (x^{(0)}(1)-\frac{\hat{b}}{\hat{a}})e^{-\hat{b}k}+\frac{\hat{b}}{\hat{a}}$
模型检验
- 模型检验就是看按照 $\hat{x}^{(1)}(k+1)$ 求得的拟合值和实际值相差大不大。
- 相对误差检验:$\epsilon(k) = \frac{|x^{(0)}(k)-\hat{x}^{(0)}(k)|}{x^{(0)}(k)}$ ,如果 $\epsilon(k)<0.2$,可认为达到一般要求;如果 $\epsilon(k)<0.1$,即达到较高要求。
- 级比偏差检验:$\rho(k)=1-\frac{1-0.5a}{1+0.5a} \lambda(k)$,其中级比 $\lambda(k) = \frac{x^{(0)}(k-1)}{x^{(0)}(k)}$,如果 $|\rho(k)|<0.2$,可认为达到一般要求;如果 $|\rho(k)|<0.1$,即达到较高要求。
原始数据的级比检验(在建模最开始进行)
为了确定原始数据使用GM(1,1)模型的可行性,避免白忙活,需要对原始数据进行级比检验:
- 计算 $\lambda(k) = \frac{x^{(0)}(k-1)}{x^{(0)}(k)},k=2,3,…,n$
如果 $\lambda(k)$ 在区间 $(e^{-\frac{2}{n+1}},e^{\frac{2}{n+2}})$,说明可用GM(1,1)模型。
- 如果在区间外,可尝试平移变换。也就是给每个数据都加上任意常数 $c$ 后,观察是否在区间内,求解后再减去 $c$ ;如果尝试多次平移变换后始终无法在区间内,说明题目不适合灰色预测。
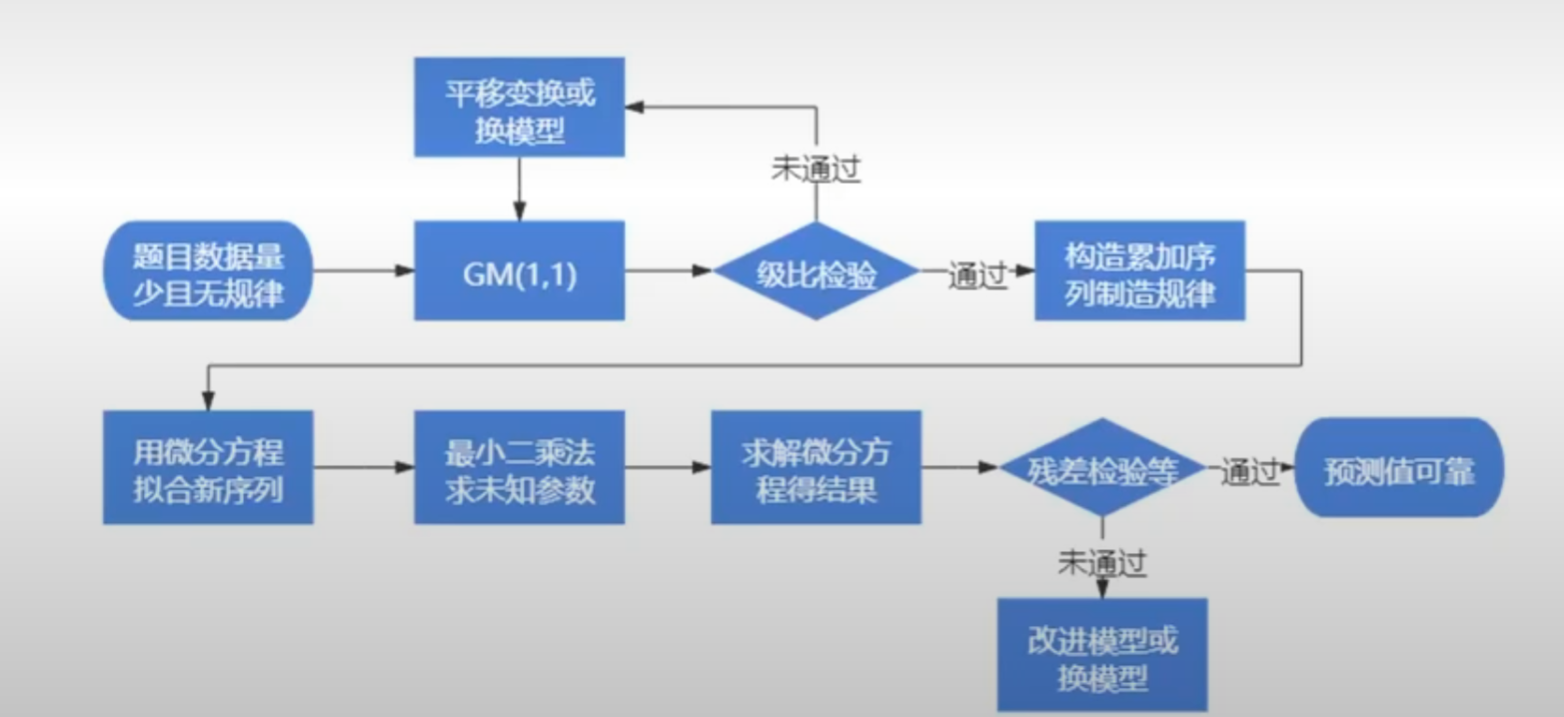
流程
核心就是最小二乘法求参数,再求微分方程。
在最开始要对原始数据进行检验,在最后要对结果进行检验。